Python数据科学：线性回归

变量分析：

①相关分析：一个连续变量与一个连续变量间的关系。

②双样本t检验：一个二分分类变量与一个连续变量间的关系。

③方差分析：一个多分类分类变量与一个连续变量间的关系。

④卡方检验：一个二分分类变量或多分类分类变量与一个二分分类变量间的关系。

本次介绍：

线性回归：多个连续变量与一个连续变量间的关系。

其中线性回归分为简单线性回归和多元线性回归。

／ 01 ／ 数据分析与数据挖掘

数据库：一个存储数据的工具。因为Python是内存计算，难以处理几十G的数据，所以有时数据清洗需在数据库中进行。

统计学：针对小数据的数据分析方法，比如对数据抽样、描述性分析、结果检验。

人工智能／机器学习／模式识别：神经网络算法，模仿人类神经系统运作，不仅可以通过训练数据进行学习，而且还能根据学习的结果对未知的数据进行预测。

／ 02 ／ 回归方程

01 简单线性回归

简单线性回归只有一个自变量与一个因变量。

含有的参数有「回归系数」「截距」「扰动项」。

其中「扰动项」又称「随机误差」，服从均值为0的正态分布。

线性回归的因变量实际值与预测值之差称为「残差」。

线性回归旨在使残差平方和最小化。

下面以书中的案例，实现一个简单线性回归。

建立收入与月均信用卡支出的预测模型。

import numpy as np

import pandas as pd

import statsmodels．api as sm

import matplotlib．pyplot as plt

from statsmodels．formula．api import ols

＃ 消除pandas输出省略号情况及换行情况

pd．set＿option（＇display．max＿columns＇， 500）

pd．set＿option（＇display．width＇， 1000）

＃ 读取数据，skipinitialspace：忽略分隔符后的空白

df ＝ pd．read＿csv（＇creditcard＿exp．csv＇， skipinitialspace＝True）

print（df．head（））

读取数据，数据如下。

对数据进行相关性分析。

＃ 获取信用卡有支出的行数据

exp ＝ df［df［＇avg＿exp＇］．notnull（）］．copy（）．iloc［：， 2：］．drop（＇age2＇， axis＝1）

＃ 获取信用卡无支出的行数据，NaN

exp＿new ＝ df［df［＇avg＿exp＇］．isnull（）］．copy（）．iloc［：， 2：］．drop（＇age2＇， axis＝1）

＃ 描述性统计分析

exp．describe（include＝＇all＇）

print（exp．describe（include＝＇all＇））

＃ 相关性分析

print（exp［［＇avg＿exp＇， ＇Age＇， ＇Income＇， ＇dist＿home＿val＇］］．corr（method＝＇pearson＇））

输出结果。

发现收入（Income）和平均支出（avg＿exp）相关性较大，值为0．674。

使用简单线性回归建立模型。

＃ 使用简单线性回归建立模型

lm＿s ＝ ols（＇avg＿exp ～ Income＇， data＝exp）．fit（）

print（lm＿s．params）

＃ 输出模型基本信息，回归系数及检验信息，其他模型诊断信息

print（lm＿s．summary（））

一元线性回归系数的输出结果如下。

从上可知，回归系数值为97．73，截距值为258．05。

模型概况如下。

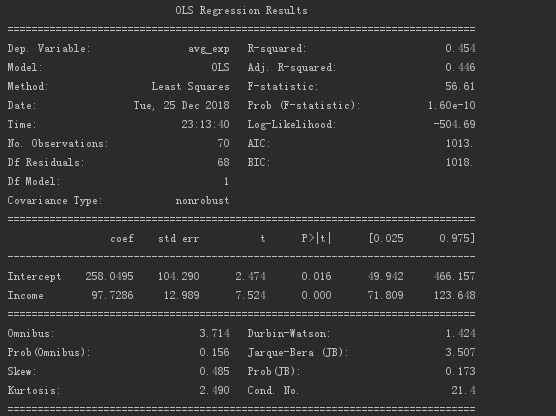
其中R值为0．454，P值接近于0，所以模型还是有一定参考意义的。

使用线性回归模型测试训练数据集，得出其预测值及残差。

＃ 生成的模型使用predict产生预测值，resid为训练数据集的残差

print（pd．DataFrame（［lm＿s．predict（exp）， lm＿s．resid］， index＝［＇predict＇， ＇resid＇］）．T．head（））

输出结果，可与最开始读取数据时输出的结果对比一下。

使用模型测试预测数据集的结果。

＃ 对待预测数据集使用模型进行预测

print（lm＿s．predict（exp＿new）［：5］）

输出结果。