Python求解插值、拟合和微分方程问题

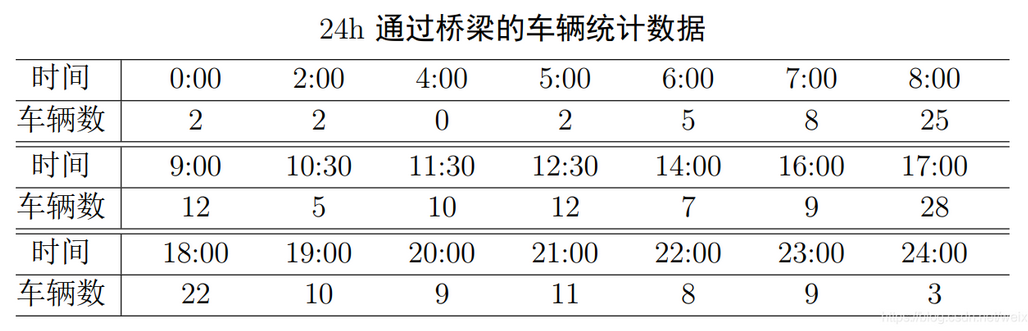
1、交通管理部门为了掌握一座桥梁的通行情况，在桥梁的一端每隔一段不等的时间连续记录1min内通过桥梁的车辆数量，连续观测一天24h的通过车辆车辆数据如下表所示。试建立模型分析估计这一天中总共有多少车辆通过这座桥梁。

代码如下：

import numpy as np

import matplotlib.pyplot as plt

from scipy.interpolate import interp1d

plt.grid(linestyle='--')       #设置网格线---这里是虚线

X = np.array([0,2,4,5,6,7,8,9,10.5,11.5,12.5,14,16,17,18,19,20,21,22,23,24])

Y = np.array([2,2,0,2,5,8,25,12,5,10,12,7,9,28,22,10,9,11,8,9,3])

xnew= np.linspace(0,24,24*60)

# 引入插值函数，这里的点较散乱，所以我选取高阶的样条插值

f=interp1d(X,Y,'quadratic'); ynew=f(xnew)

plt.plot(xnew,ynew,c='b')

plt.show()

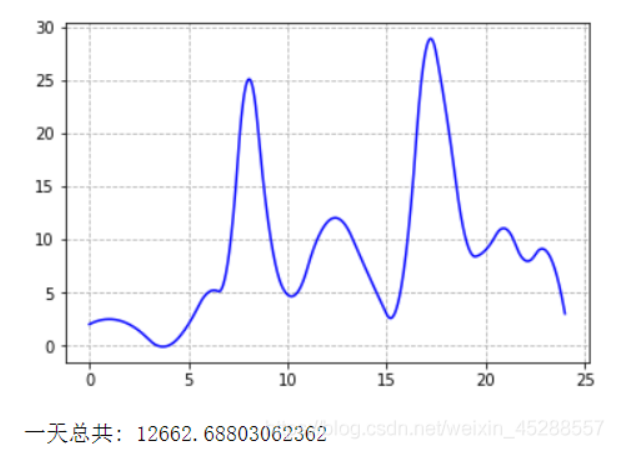
# 计算一天的车辆总数

c=sum(ynew)

print('一天总共:',c)

2、某年美国旧车价格的调查资料如下表所示，其中xi表示轿车的使用年数，yi表示相应的平均价格．试分析用什么形式的曲线拟合表中所给的数据，并预测使用4．5年后轿车的平均价格大致为多少？

代码如下：

import matplotlib.pyplot as plt

import numpy as np

from numpy import polyfit,polyval

x=np.linspace(0,10,11)[1:11]

y=np.array([2615,1943,1494,1087,765,538,484,290,226,204])

p=polyfit(x,y,2)

print('p:',p)

ynew=polyval(p,x)

plt.plot(x,ynew)

plt.show()

ypred=polyval(p,4.5)

print('使用4.5年后轿车的平均价格大致为:',ypred)

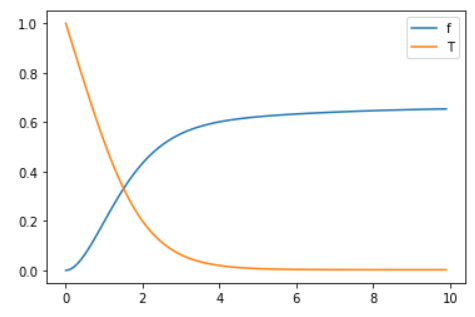
3、求下列微分方程组（竖直加热板的自然对流）的数值解

代码如下：

import matplotlib.pyplot as plt

import numpy as np

from scipy.integrate import odeint

def fT(y,x):

    f,df,ddf,T,dT=y; #拆分、降阶

    return np.array([df,ddf,2*(df*df)-T-3*f*ddf,dT,-2.1*f*dT])

x=np.arange(0,10,0.1)

ynew=odeint(fT,[0.0,0.0,0.68,1.0,-0.5],x)

#plt.rc('font',size=16);plt.rc('font',family='Times New Roman')

plt.plot(x,ynew[:,0],label='f')

plt.plot(x,ynew[:,3],label='T')

plt.legend()

plt.show()

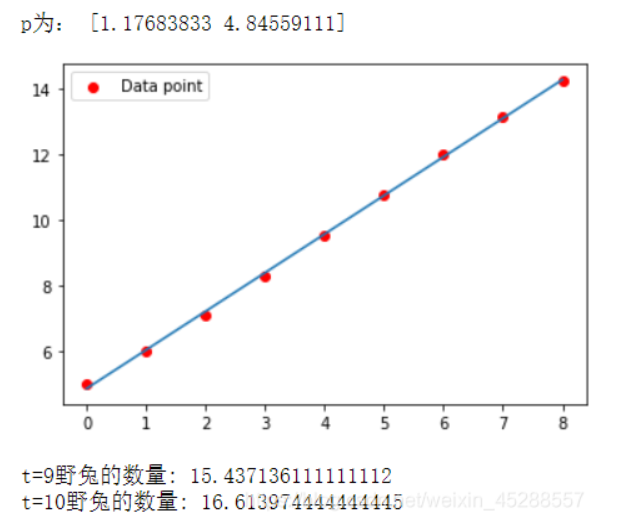
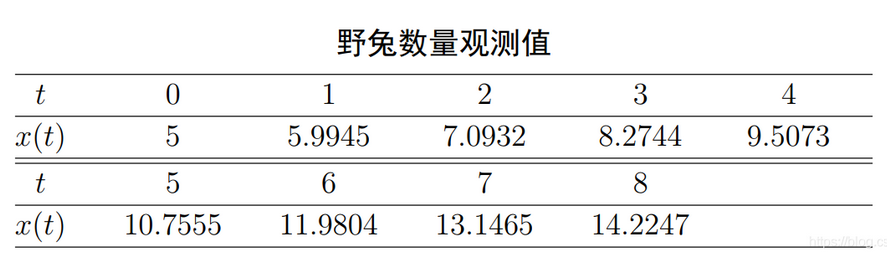
4、某地区野兔的数量连续9年的统计数量（单位：十万）如下表所示。预测t＝9，10时野兔的数量。

代码如下：

import matplotlib.pyplot as plt

import numpy as np

x=np.linspace(0,8,9)

y=np.array([5,5.9945,7.0932,8.2744,9.5073,10.7555,11.9804,13.1465,14.2247])

plt.scatter(x,y,c='r',label='Data point')

p=np.polyfit(x,y,1)

print('p为：',p)

ynew1=np.polyval(p,x)

plt.plot(x,ynew1)

plt.legend()

plt.show()

#从图中可以看出一次多项式的拟合效果就很好，所以接下来预测时采用一次多项式即可

y9=np.polyval(p,9)

y10=np.polyval(p,10)

print('t=9野兔的数量:',y9)

print('t=10野兔的数量:',y10)