自动驾驶汽车路径规划算法浅析

自动驾驶汽车的路径规划算法最早源于机器人的路径规划研究，但是就工况而言却比机器人的路径规划复杂得多，自动驾驶车辆需要考虑车速、道路的附着情况、车辆最小转弯半径、外界天气环境等因素。

本文将为大家介绍四种常用的路径规划算法，分别是搜索算法、随机采样、曲线插值和人工势场法。

1．搜索算法

搜索算法主要包括遍历式和启发式两种，其中Dijkstra算法属于传统的遍历式，A＊算法属于启发式，在A＊算法的基础上，还衍生出了D＊Lite算法、Weighted A＊算法等其他类型。Dijkstra算法最早由荷兰计算机学家狄克斯特拉于1959年提出，算法核心是计算从一个起始点到终点的最短路径，其算法特点是以起始点开始向周围层层扩展，直到扩展到终点为止，再从中找到最短路径，算法搜索方式如图（1－1）所示。A＊算法在Dijkstra算法上结合了最佳优先算法，在空间的每个节点定义了一个启发函数（估价函数），启发函数为当前节点到目标节点的估计值，从而减少搜索节点的数量从而提高效率。A＊算法中的启发函数包括两部分，表示从初始点到任意节点n的代价，表示节点n到目标点的启发式评估代价，在对象从初始点开始向目标点移动时，不断计算的值，从而选择代价最小的节点。一般来说遍历式算法可以取得全局最优解，但是计算量大，实时性不好；启发式算法结合了遍历式算法以及最佳优先算法的优点，具有计算小、收敛快的特点。图（1－2）是最佳优先算法示意图，可以看出该算法有一定的选择性，但是面对图中的u型障碍物会出现计算效率低的情况。而A＊算法完美的结合了Dijkstra算法和最佳优先算法，不仅有一定的选择性，并且计算量相对也是最少的，更快得找到了最短路径。

图1－1 Dijkstra算法示意图

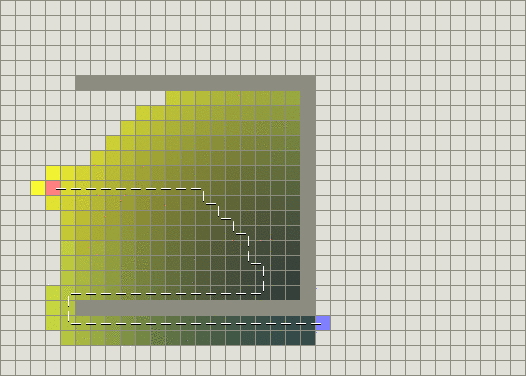
图1－2 最佳优先算法示意图

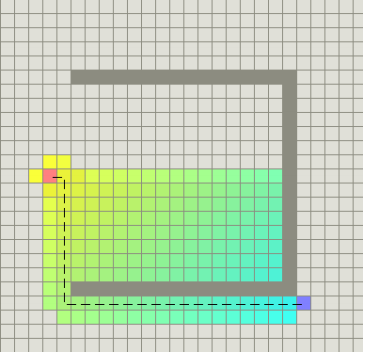
图1－3 A＊算法示意图

2．随机采样

随机采样主要包括蚁群算法以及RRT（快速扩展随机树）算法。蚁群算法是由Dorigo M等人于1991年首先提出，并首先使用在解决TSP（旅行商问题）上。其算法基本原理如下：1．蚂蚁在路径上释放信息素。2．碰到还没走过的路口，随机选一条走，同时释放与路径长度有关的信息素。3．信息素浓度与路径长度成反比。后来蚂蚁再次碰到该路口时，就选择信息浓度较高的路径。4．最优路径上的信息素浓度越来越大。5．信息素浓度最大的路径为最优路径。其在小规模TSP中性能尚可，再大规模TSP问题中性能下降，容易停滞。实际道路环境是比较复杂的，不光有道路、障碍物等的限制，也有其自身动力学的约束，所以该算法更适合做全局路径规划，不太适合局部路径规划。

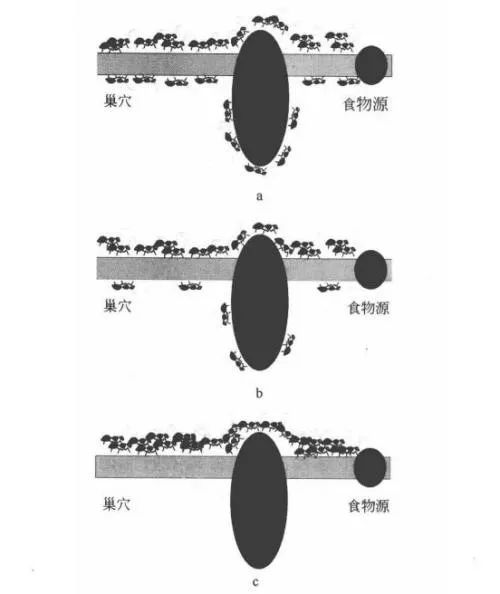
图2－1 蚁群算法示意图

3．曲线插值

曲线插值的方法是按照车辆在某些特定条件（安全、快速、高效）下，进行路线的曲线拟合，常见的有贝塞尔曲线、多项式曲线、B样条曲线等。一般就多项式算法而言，主要考虑以下几个几何约束，从而确定曲线的参数。几何约束：1．起始点的位置与姿态。2．最小转弯半径。3．障碍物约束。4．目标点的位置与姿态。根据考虑的几何约束不同，多项式算法的阶数从三阶到六阶甚至更高阶，阶数越高的算法复杂度越高，收敛速度越慢。四次多项式的形式如式（3－1）所示，参数由几何约束条件确定。基于参数化曲线来描述轨迹，这种类型的算法比较直观，也可以更加准确的描述车辆所需满足的道路条件，规划出的轨迹也十分平坦、曲率变化连续并可进行约束。缺点是计算量较大，实时性不太好，并且其评价函数也比较难以找到最优的，未来的研究方向主要集中于简化算法以及更加完善的评价函数。目前，曲线拟合算法是采用比较广泛的规划方法。

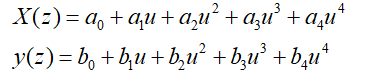
       （3－1）

4．人工势场法

人工势场法（Artificial PotentialField，APF）是由Khatib于1986年提出的。该算法是假设目标点会对自动驾驶车辆产生引力，障碍物对自动驾驶车辆产生斥力，从而使自动驾驶车辆沿“势峰”间的“势谷”前进。这种算法的优点就是结构简单，有利于底层控制的实时性，可大大减少计算量和计算时间，并且生成相对光滑的路径，利于保持自动驾驶车辆的稳定性。算法的缺点是有可能陷入局部最优解，难以对规划出的路径进行车辆动力学约束，复杂环境下的势场搭建也比较棘手。势场的基本步骤如下：首先搭建势场，包括障碍物势场以及目标点势场，然后通过求势场负梯度，可以得到车辆在势场中所受的障碍物斥力以及目标点引力。将所受的所有障碍物斥力与目标点引力叠加，就可以得到车辆在势场中任意位置的受力情况，最后根据合力情况不断迭代更新位置，就可以得到从起始点到终点的完整路径。

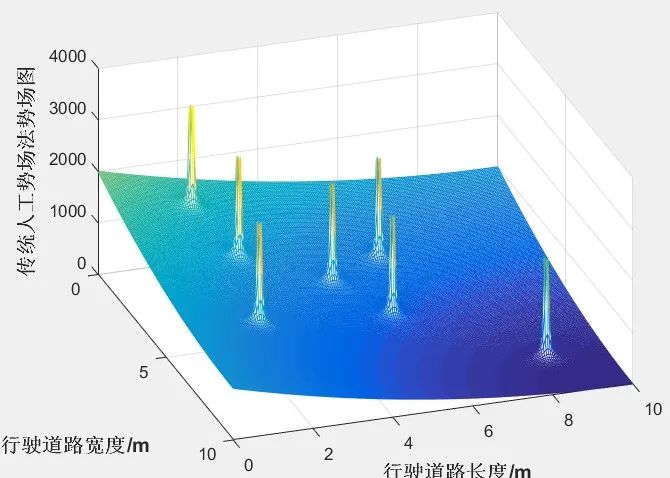
图4－1 基于人工势场法搭建的势能场

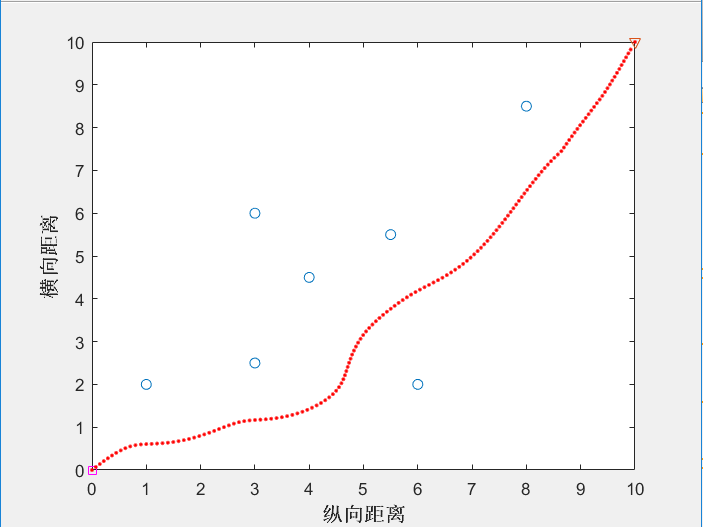
图4－2 基于人工势场法规划的路径点

最后以下表对本文介绍的四种算法的优缺点、计算效率进行一个简要的对比总结。不难发现，其中人工势场法的计算速度最快，实时性也最好，但是存在局部最优解、复杂势场难以搭建的情况，这也是未来该算法的研究热点、难点；其中，曲线插值是目前较常见的一种算法，虽然该算法的计算效率不高，但是相信在未来车载计算机的计算能力大幅度提升之后，该算法可以被更广泛得使用。