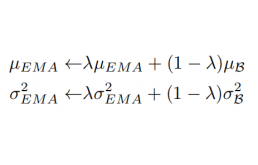一文带你重新思考BatchNorm中的Batch

前言

公众号在前面发过三篇分别对BatchNorm解读、分析和总结的文章(文章链接在文末),阅读过这三篇文章的读者对BatchNorm和归一化方法应该已经有了较深的认识和理解。在本文将介绍一篇关于BatchNorm举足轻重的论文,这篇论文对进行了很多实验,非常全面地考虑了BatchNorm中的Batch。

欢迎关注公众号 CV技术指南 ,专注于计算机视觉的技术总结、最新技术跟踪、经典论文解读。

Motivation

BatchNorm 区别于其他深度学习算子的关键因素是它对批量数据而不是单个样本进行操作。BatchNorm 混合批次中的信息以计算归一化统计数据,而其他算子独立处理批次中的每个样本。因此,BatchNorm 的输出不仅取决于单个样本的属性,还取决于样本分组的方式。

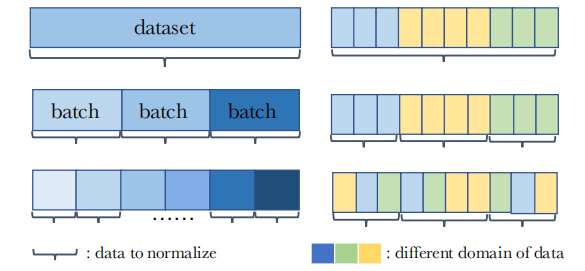
如上左图所示,按照采样大小,上中下三图表示BatchNorm的采样方式分别为entire dataser、mini-batches和subset of mini-batches。

如上右图所示,按照采样风格,上中下三图表示BatchNorm的采样方式分别为entire domain、each domain和mixture of each domain。

论文研究了 BatchNorm 中批处理的这些选择,证明了在不考虑批处理构建的不同选择的情况下,应用批处理规范可能会在许多方面产生负面影响,但可以通过在批处理方式上做出谨慎选择来提高模型性能。

Review of BatchNorm

在一个mini-batches中,在每一BN层中,对每个通道计算它们的均值和方差,再对数据进行归一化,归一化的值具有零均值和单位方差的特点,最后使用两个可学习参数gamma和beta对归一化的数据进行缩放和移位。

此外,在训练过程中还保存了每个mini-batches每一BN层每一通道的均值和方差,最后求所有mini-batches均值和方差的期望值,以此来作为推理过程中该BN层各自通道的均值和方差。

Whole Population as a Batch

在训练期间,BatchNorm 使用mini-batch的样本计算归一化统计数据。但是,当模型用于测试时,通常不再有 mini-batch 的概念。最初提出BatchNorm是在测试时,特征应该通过在整个训练集上计算的总体统计数据 μ、σ 进行归一化。这里的 μ、σ 被定义为批次统计量 ?, σ 使用整个population作为“Batch”。

广泛使用EMA 算法来计算 ?, σ,但它并不总是能准确地训练population数据,因此论文提出了新的算法PreciseBN。

Inaccuracy of EMA

EMA: exponential moving average

算法公式如下:

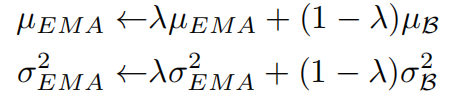
由于以下原因,EMA会导致模型估计Population数据次优:

当 λ 很大时,统计数据收敛缓慢。由于每次更新迭代仅对 EMA 贡献一小部分 (1-λ),因此 EMA 需要大量更新才能收敛到稳定的估计值。随着模型的更新,情况变得更糟:EMA 主要由过去的输入特征主导,随着模型的训练这些特征已经过时。

当 λ 较小时,EMA 统计数据由较少数量的近期mini-batch主导,并不代表整个populatioin。

PreciseBN

PreciseBN通过以下两个步骤来近似Population统计数据。

(固定)模型在许多小批量上应用来收集Batch统计数据;

将per-batch统计数据聚合为总体统计数据。

与EMA相比,PreciseBN多了两个重要的属性:

统计数据完全根据固定模型状态计算,与使用模型历史状态的 EMA 不同;

所有样本的权重相等。

实验结论

1．PreciseBN比BN更稳定。

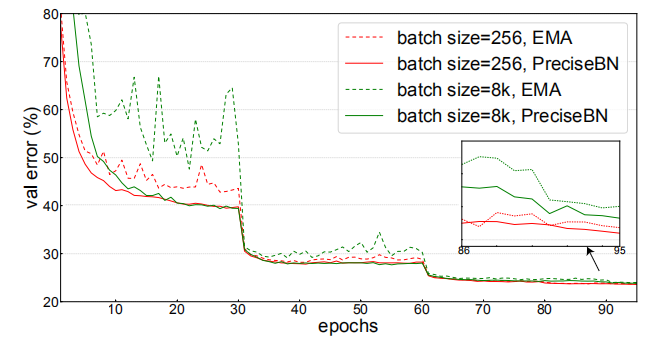
2．当batchsize很大时,EMA算法不稳定。作者认为不稳定性是由大批量训练中损害 EMA 统计收敛性的两个因素造成的:(1)32 倍大的学习率导致特征发生更剧烈的变化;(2) 由于总训练迭代次数减少,EMA 的更新次数减少了 32 倍。

3．PreciseBN只需要个样本就可以得到稳定的结果。

4．小Batch会累计误差。

Batch in Training and Testing

在训练和推理期间使用的Batch统计量不一致:训练期间使用mini-batch统计数据,推理期间使用训练期间所有mini-batch通过EMA算法近似得到的population统计数据。论文分析了这种不一致对模型性能的影响,并指出在某些情况下可以轻松消除不一致以提高性能。

为了避免混淆,将SGD batch size或者total batch size定义为所有GPU上总的batch size大小,将normalization batch size定义为单个GPU上的batch size大小。(注:这一点在《归一化方法总结》一文中有提到,当使用多个GPU时,实际的mini-batch统计数据只基于batchsize/GPU数的样本上统计)

normalization batch size对训练噪声和训练测试不一致性有直接影响:较大的Batch将mini-batch统计数据推向更接近总体统计数据,从而减少训练噪声和训练测试不一致

为了便于分析,论文观察了3种不同评估方法的错误率:

在训练集上对mini-batch统计量进行评估

在验证集上对mini-batch统计量进行评估

在验证集上对population统计量进行评估

实验结论

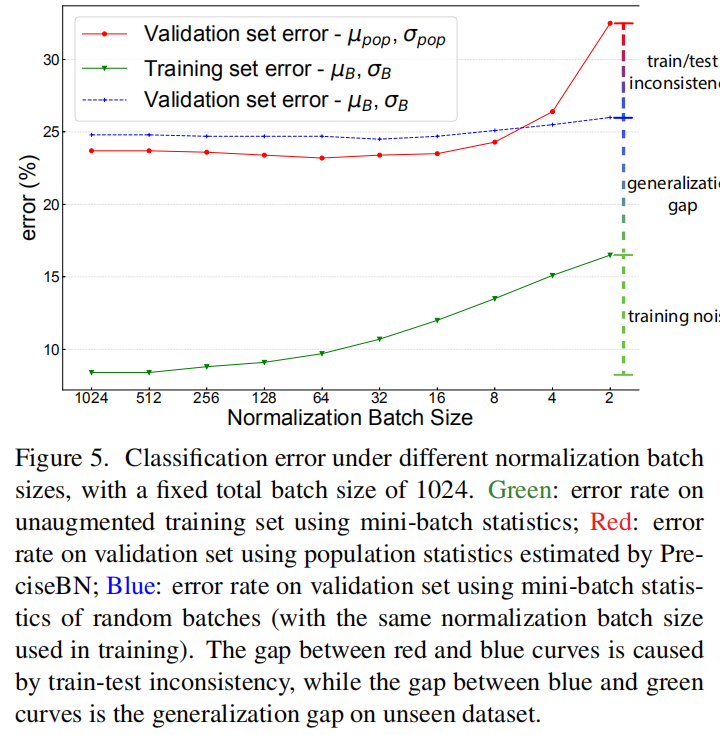
小的normalization batch size(例如 2 或 4)性能不佳,但如果使用mini-batch统计数据(蓝色曲线),该模型实际上具有不错的性能。结果表明,mini-batch统计和总体统计之间的巨大不一致是影响mini-batch性能的主要因素。

另一方面,当normalization batch size较大时,小的不一致可以提供正则化以减少验证错误。这导致红色曲线比蓝色曲线表现更好。

基于以上结论,论文给出两个消除不一致用来提高性能的方法

Use Mini-batch in Inference

Use Population Batch in Training

Batch from Different Domains

BatchNorm 模型的训练过程可以被视为两个独立的阶段:首先通过 SGD 学习特征,然后通过 EMA 或 PreciseBN 使用这些特征训练总体统计数据。我们将这两个阶段称为“SGD training”和“population statistics training”。

在本节中,论文分析出现domain gap的两种情况:当模型在一个domain上训练但在其他domain上测试时,以及当模型在多个domain上训练时。这两者都会使 BatchNorm 的使用复杂化。

实验结论

1. 当存在显着的域偏移时,模型在对评估中使用的domain会比使用 SGD 训练,进行总体统计训练后获得最佳错误率。直观地说,根据domain组成Batch可以减少训练测试的不一致并提高对新数据分布的泛化能力。

2. BatchNorm 在mixture of multi-domain data上的domain-specific training在以前的工作中经常被提出,名称为“Domain-Specific BN”、“Split BN”、“Mixture BN”,“Auxiliary BN”,“Transferable Norm”。这些方法都包含以下三种选择中的一些。

Domain-specific SGD training

Domain-specific population statistics

Domain-specific affine transform

通过消除上述三个选择,我们表明在 SGD training和population statistics training之间使用一致的策略很重要,尽管这种实现可能看起来不直观。

Information Leakage within a Batch

我在《归一化方法总结》中总结到,BN的三个缺陷之一便是当mini-batch中的样本非独立同分布时,性能比较差,作者认为这是由于Information Leakage导致的。

论文实验发现,当使用random采样的mini-batch统计量时,验证误差会增加,当使用population统计量时,验证误差会随着epoch的增加逐渐增大,验证了BN信息泄露问题的存在。

为了处理信息泄露问题,之前常见的做法是使用SyncBN,来弱化mini-batch内样本之间的相关性。另一种解决方法是在进入head之前在GPU之间随机打乱RoI features,这给每个GPU分配了一个随机的样本子集来进行归一化,同时也削弱了min-batch样本之间的相关性,如下图所示。

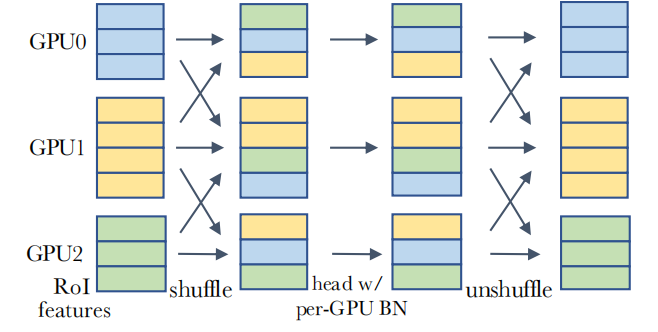
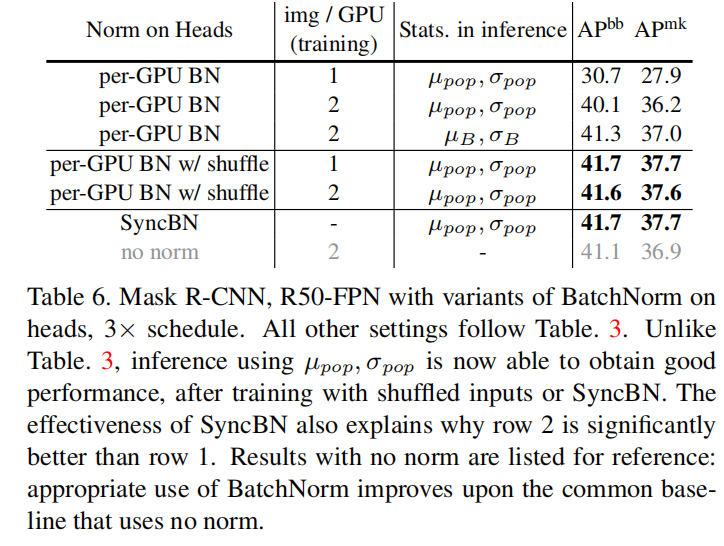
如下图所示,实验证明 shuffling和 SyncBN 都有效地解决了信息泄漏问题,允许head在测试时很好地概括population statistics。

在速度方面,对于深度模型,shuffle 需要较少的 cross-GPU 同步,但每次同步传输的数据比 SyncBN 层传输的数据多。因此,它们的相对效率因模型架构而异。据比SyncBN多。因此,shuffling和SyncBN的相对效率跟具体模型架构相关。

总结

本文回顾了BatchNorm算法;分析了使用mini-batches计算的统计数据和基于population作为batch计算的统计数据的效果,提出了PreciseBN近似统计算法,该算法相比于常用的EMA算法有更稳定的效果;分析了根据不同domain来组成mini-batch的效果差异;分析了处理mini-batch中的样本非独立同分布情况的两种方法。

结合前面的三篇文章《Batch Normalization》、《可视化的BatchNorm--它的工作方式以及为什么神经网络需要它》、《归一化方法总结 | 又名"BN和它的后浪们"》,相信读者会对BatchNorm会有一个非常全面的认识,并进一步加深对神经网络的理解。

本文来源于公众号 CV技术指南 的论文分享系列。

欢迎关注公众号 CV技术指南 ,专注于计算机视觉的技术总结、最新技术跟踪、经典论文解读。