什么是梯度下降，为什么它很重要？

梯度下降是有时会吓到初学者和从业者的话题之一。大多数人在听到梯度这个词时,他们试图在不了解其背后的数学的情况下完成该主题。本文,将从一个非常基础的层面解释梯度下降,并用简单的数学示例为你提供帮助,并使梯度下降完全为你所用。

目录

什么是梯度下降,为什么它很重要?

梯度下降背后的直觉

梯度下降背后的数学

具有 1 个变量的梯度下降代码

具有 2 个变量的梯度下降

学习率的影响

损失函数的影响

数据效果

尾注

什么是梯度下降?

梯度下降是一种用于寻找局部最小值或优化损失函数的一阶优化技术。它也被称为参数优化技术。

为什么是梯度下降?

使用封闭形式的解决方案很容易找到斜率和截距的值,但是当你在多维数据中工作时,该技术成本太高,并且需要大量时间,因此它在这里失败了。因此,新技术以梯度下降的形式出现,它可以非常快速地找到最小值。梯度下降不仅适用于线性回归,而且是一种可以应用于任何机器学习部分的算法,包括线性回归、逻辑回归,它是深度学习的完整支柱。梯度下降背后的直觉考虑到我有一个包含CGPA和薪资待遇的学生数据集。

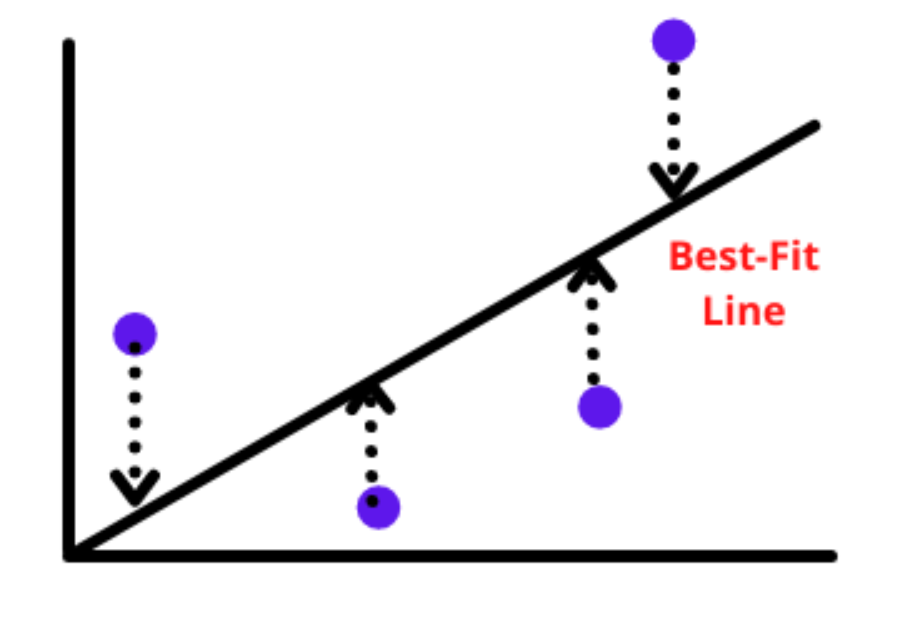
我们必须找到最佳拟合直线,当损失最小时,给出b的最小值。损失函数定义为实际值和预测值之间的差的平方和。

为了使问题更容易理解,假设给定 m 的值,我们必须预测截距(b)的值。所以我们想找出 b 的最小值,其中 L(loss) 应该是最小值。因此,如果我们绘制 L 和 b 之间的图形,那么它将是一个抛物线形状。现在在这个抛物线中,我们必须找到使损失最小的 b 的最小值。如果我们使用普通最小二乘法,它会微分并等于零。但这对于处理高维数据并不方便。所以,这里出现了梯度下降。让我们开始执行梯度下降。

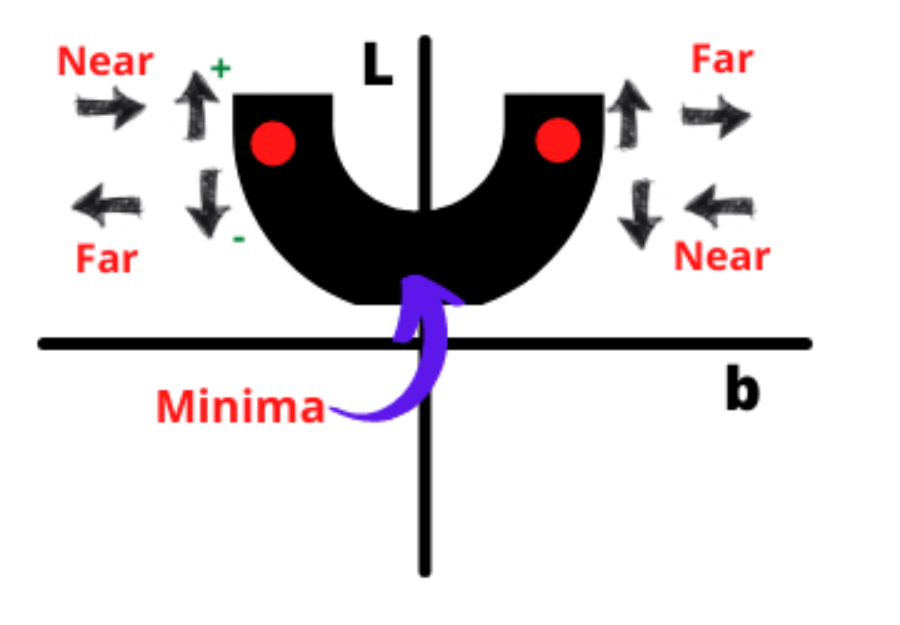
选择一个随机值 b

我们选择 b 的任意随机值并找到其对应的 L 值。现在我们想把它收敛到最小值。

在左侧,如果b 增加,则我们将趋于最小值,如果b减小,则我们将远离最小值。

在右侧,如果 b减小,那么我们将接近最小值,而在b增加时,则将远离最小值。

现在我怎么知道我想前进还是后退?所以,答案很简单,我们找到我们当前所在点的斜率。

现在问题又来了,怎么求斜率?为了找到斜率,我们对方程 os 损失函数进行求导,即斜率方程,简化后我们得到一个斜率。现在斜率的方向将指示你必须向前或向后移动。如果斜率是正的,那么我们必须减小 b,反之亦然。简而言之,我们用原来的截距减去斜率来求新的截距。

b_new = b_old - slope
这只是梯度方程,如果你有多个变量作为斜率和截距,则梯度表示导数。

现在再次出现的问题是,**我怎么知道在哪里停下来?**我们将在循环中多次执行此收敛步骤,因此有必要知道何时停止。还有一件事是,如果我们减去斜率,则运动会发生剧烈变化,这被称为之字形运动。为了避免这种情况,我们将斜率乘以一个非常小的正数,称为学习率。

现在方程是b_new = b_old - learning rate * slope
因此,这就是为什么我们使用学习率来减少步长和运动方向的剧烈变化。在本教程中,我们将更深入地了解学习率的作用和使用。现在的问题是什么时候停止循环?当我们停止时有两种方法。

当 b_new – b_old = 0 表示我们没有前进,所以我们可以停下来。我们可以将迭代次数限制为 1000 次。多次迭代称为 epoch,我们可以将其初始化为超参数。这就是梯度下降背后的直觉。我们只介绍了理论部分,现在我们将开始梯度下降背后的数学,我很确定你会很容易地掌握它。梯度下降背后的数学考虑一个数据集,我们不知道初始截距。我们想预测 b 的最小值,现在,已知 m 的值。我们必须应用梯度下降来获取 b 的值。其背后的原因是理解一个变量,在本文中,我们将同时使用b和m来实现完整的算法。

步骤1)从随机b开始

一开始,我们考虑 b 的任何随机值并在 for 循环中开始迭代,并在斜率的帮助下找到 b 的新值。现在假设学习率为 0．001,epochs 为 1000。

步骤2) 运行迭代

for i in epochs:
 b_new = b_old - learning_rate * slope
现在我们要计算 b 的当前值处的斜率。因此,我们将借助损失函数,通过对b求导来计算斜率方程。

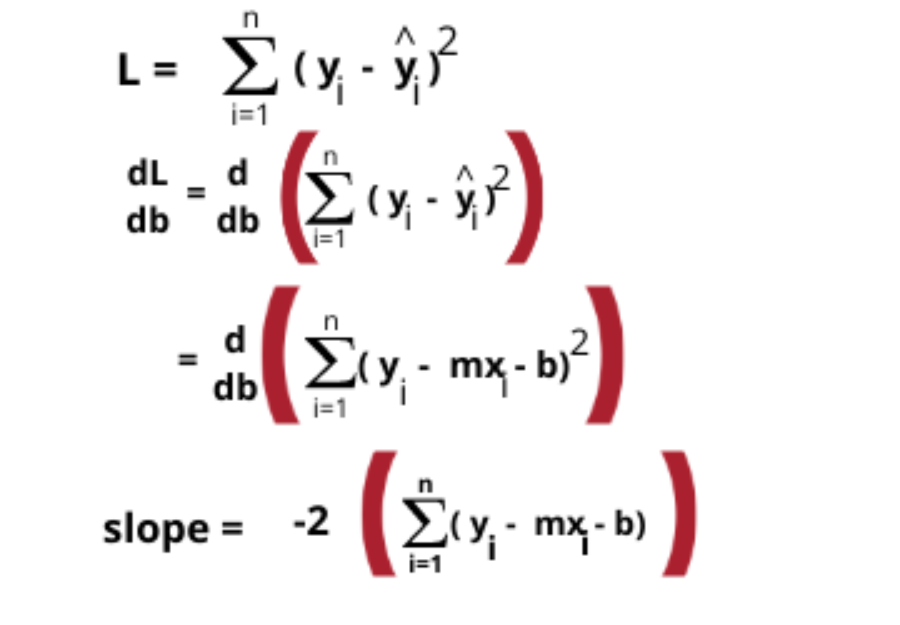
这很简单,它正在计算斜率,你只需输入值并计算斜率即可。m 的值已知,所以它更容易。我们会做这件事,直到所有的迭代都结束。我们已经看到了梯度下降是如何工作的,现在让我们用Python来实现梯度下降。具有1个变量的梯度下降代码在这里,我创建了一个非常小的数据集,有四个点来实现梯度下降。并且我们给出了 m 的值,因此我们将首先尝试普通最小二乘法来获得 m,然后我们将在数据集上实现梯度下降。from sklearn．datasets import make_regression
import numpy as np
import matplotlib．pyplot as plt
X,y = make_regression(n_samples=4, n_features=1, n_informative=1, n_targets=1, noise=80, random_state=13)
plt．scatter(X,y)

使用OLS获取m的值

from sklearn．linear_model import LinearRegression
reg = LinearRegression()
reg．fit(X,y)
print(reg．coef_)
print(reg．intercept_)
应用OLS后,我们得到系数,m值为78．35,截距为26．15。现在我们将通过取截距的任何随机值来实现梯度下降,你会看到在执行 2 到 3 次迭代后,我们将达到 26．15 附近,这就是我们要实现的最终目标。如果我通过 OLS 绘制预测线,则它看起来像这样。

plt．scatter(X,y)
plt．plot(X,reg．predict(X),color='red')

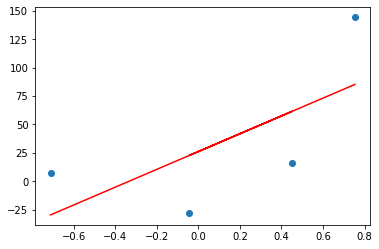
现在我们将实现梯度下降,然后你将看到我们的梯度下降预测线将随着迭代的增加而重叠。

迭代1

让我们应用梯度下降,假设斜率恒定在78．35,并且截距b的起始值为0。因此,让我们应用方程式并预测初始值。y_pred = ((78．35 * X) + 0)．reshape(4)
plt．scatter(X,y)
plt．plot(X,reg．predict(X),color='red',label='OLS')
plt．plot(X,y_pred,color='#00a65a',label='b = 0')
plt．legend()
plt．show()

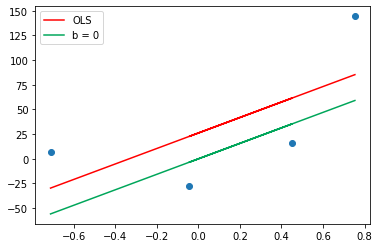
这是一条截距为0的直线,现在我们继续计算斜率,找到一个新的b值,它会向红线移动。m = 78．35
b = 0
loss_slope = -2 * np．sum(y - m*X．ravel() - b)
# Lets take learning rate = 0．1
lr = 0．1
step_size = loss_slope*lr
print(step_size)
# Calculating the new intercept
b = b - step_size
print(b)
当我们计算学习率乘以斜率时,称为步长,为了计算新的截距,我们从旧的截距中减去步长,这就是我们所做的。新的截距是 20．9,因此我们直接从 0 到达了 20．9。

迭代–2

现在,我们将再次计算截距 20 处的斜率,你将看到它将非常接近所需的截距 26．15。代码与上面相同。loss_slope = -2 * np．sum(y - m*X．ravel() - b)
step_size = loss_slope*lr
b = b - step_size
print(b)
现在截距为 25．1,非常接近所需的截距。如果你再运行一次迭代,那么我相信你将获得所需的截距,并且绿线将超过红线。在绘图时,你可以看到如下图,其中绿线超过了红线。

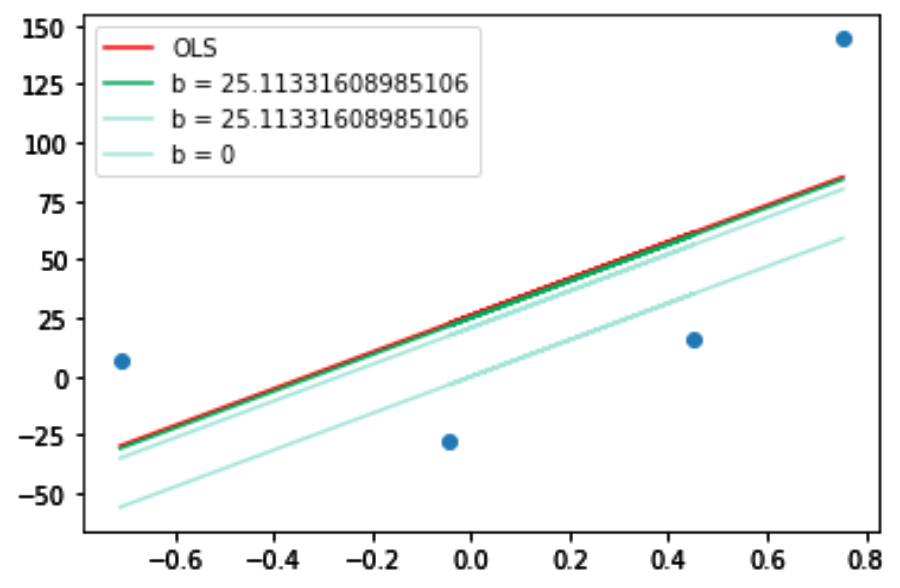
从上面的实验中,我们可以得出结论,当我们远离最小值时,我们会走大步,而当我们接近最小值时,我们会走小步。这就是梯度下降的美妙之处,即使你从任何错误的点开始,比如 100,然后经过一些迭代,你也会到达正确的点,这都归功于学习率。2个变量的梯度下降现在我们可以理解梯度下降的完整工作原理了。我们将使用变量 m 和 b 执行梯度下降,m与b都未知。

Step-1) 初始化m和b的随机值

在这里,我们初始化任何随机值,例如 m 为 1,b 为 0。

Step-2)初始化epoch数和学习率

将学习率尽可能小,假设 学习率为0．01 和 epochs 为 100

Step-3) 在迭代中开始计算斜率和截距

现在我们将在几个时期应用一个循环并计算斜率和截距。for i in epochs:
 b_new = b_old - learning_rate * slope
 m_new = m_old - learning_rate * slope
该方程与我们上面通过求导推导出的方程相同。在这里,我们必须对等式进行 2 次求导。一个关于 b(截距),一个关于 m。这就是梯度下降。现在,我们将使用Python为这两个变量构建梯度下降完整算法。用 Python 实现完整的梯度下降算法from sklearn．datasets import make_regression
X, y = make_regression(n_samples=100, n_features=1, n_informative=1, n_targets=1, noise=20, random_state=13)
这是我们创建的数据集,现在你可以自由应用 OLS 并检查系数和截距。让我们建立一个梯度下降类。class GDRegressor:
 def __init__(self, learning_rate, epochs):
   self．m = 100
   self．b = -120
   self．lr = learning_rate
   self．epochs = epochs
 def fit(self, X, y):
   #calculate b and m using GD
   for i in range(self．epochs):
     loss_slope_b = -2 * np．sum(y - self．m * X．ravel() - self．b)
     loss_slope_m = -2 * np．sum((y - self．m * X．ravel() - self．b)*X．ravel())
     self．b = self．b - (self．lr * loss_slope_b)
     self．m = self．m - (self．lr * loss_slope_m)
   print(self．m, self．b)
 def predict(self, X):
   return self．m * X + self．b
#create object and check algorithm
gd = GDRegressor(0．001, 50)
gd．fit(X, y)
因此,我们从头开始实现了完整的梯度下降。学习率的影响学习率是梯度下降中一个非常关键的参数,应该通过实验两到三次来明智地选择。如果你设置学习率为一个非常高的值,那么将永远不会收敛,并且斜率将从正轴跳到负轴。

学习率总是设置为一个小的值以快速收敛。损失函数的影响一个是学习率,我们已经看到了它的影响,接下来影响梯度下降的是损失函数。我们在本文中使用了均方误差,这是一个非常简单且最常用的损失函数。这个损失函数是凸的。凸函数是一个函数,如果你在两点之间画一条线,那么这条线永远不会与这个函数相交,这就是所谓的凸函数。梯度下降总是一个凸函数,因为在凸函数中只有一个最小值。

数据的影响

数据影响梯度下降的运行时间。如果数据中的所有特征都在一个共同的尺度上,那么它收敛得非常快,等高线图恰好是圆形的。但是如果特征尺度相差很大则收敛时间太长,你会得到一个更平坦的轮廓。尾注我们已经从头学习了梯度下降,并用一个和两个变量构建它。

它的美妙之处在于,无论你从任何奇怪的点开始,它都能让你找到正确的点。梯度下降用于大多数机器学习,包括线性和逻辑回归、PCA、集成技术。